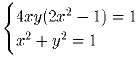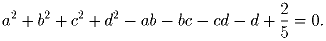Задача 1:
Решить систему уравнений:
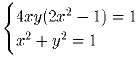
Задача 2:
На ребрах произвольного тетраэдра указали направления. Может
ли сумма полученных таким образом шести векторов оказаться
равной нуль-вектору?
Задача 3:
Функция f задана на всей вещественной оси, причем для любого x
имеет место равенство: f(x + 1)f(x) + f(x + 1) + 1 = 0. Доказать, что f не
может быть непрерывной.
Задача 4:
Найдите вещественные числа a, b, c, d, если известно, что
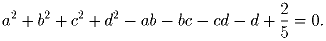
Задача 5:
AM, BN, CP – высоты остроугольного треугольника ABC.
Доказать,
что MN • NP • MP = AN • BP • CM.