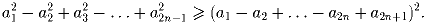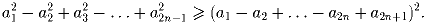Задача 1:

Задача 2: На сторонах произвольного треугольника ABC произвольным образом выбраны точки M, N и P. Через M₁, N₁ и P₁ обозначены точки, симметричные точкам M, N и P относительно середин этих сторон. Докажите, что треугольники MNP и M₁N₁P₁ равновелики.

Задача 3: Множество A, состоящее из вещественных чисел, обладает следующим свойством: вместе с числом x оно содержит число 2x² – 1. Может ли A содержать ровно 100 чисел?

Задача 4: Биссектрисы AA₁ и BB₁ треугольника ABC пересекаются в точке O. Докажите, что если угол C треугольника равен 60  , то OA₁ = OB₁.

Задача 5: Дана невозрастающая последовательность неотрицательных чисел a₁ ≥ a₂ ≥  …  ≥ a_2n + 1 ≥ 0. Докажите неравенство: