Задача 1:
Операция *, примененная к паре положительных чисел a и b, дает
число a*b. Известно, что a*1 = a,a*a = 1 для любого a, а также
(a*b) • (c*d) = (ac) • (bd) для любых a,b,c,d.
Чему равно число 27*243?
Задача 2:
Задача 3:
Вычислите:
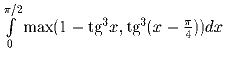
.
Задача 4:
На числовой оси задана трижды дифференцируемая функция f, для
которой f(x) • f′(x) • f′′(x) = 0 в любой точке x.
Докажите, что f –
линейная функция.
Задача 5:
Четыре сферы, центры которых не лежат в одной плоскости,
попарно пересекаются по окружностям. Докажите, что все шесть
плоскостей, в которых лежат окружности пересечений, пересекаются
в одной точке (центры никаких трех сфер не лежат на одной
прямой).


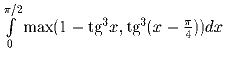 .
.