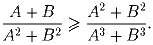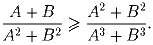Задача 1:

Задача 2: Коля и Вася получили за сентябрь по 64 оценки, причем Коля получил пятерок столько же, сколько Вася – четверок, четверок столько же, сколько Вася – троек, троек столько же, сколько Вася – двоек и двоек столько же, сколько Вася – пятерок. Кроме того оказалось, что их средние баллы совпадают. Сколько у Коли двоек?

Задача 3: Отрезок, соединяющий середины противоположных сторон AB и CD выпуклого четырехугольника ABCD, делится точкой пересечения с диагональю AC пополам. Докажите, что площади треугольников ABC и ACD равны.

Задача 4: Пусть A и B – положительные числа. Докажите, что