Задача 1: На каждом из шести изображенных на рисунке отрезков стоит натуральное число. К любым трем числам, чьи отрезки образуют треугольник, можно одновременно прибавить 1. Докажите, что можно сделать так, чтобы суммы чисел, стоящих на сторонах любого из этих четырех треугольников, давали одинаковый остаток при делении на 3.

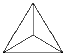
(Д.~Карпов)

Задача 2: В войске герцога Икторна 1000 гоблинов. Любые два гоблина либо дружат, либо враждуют, либо незнакомы. Гоблины – существа малообщительные, разговаривают только с друзьями. К тому же все они в плохом настроении, поскольку у каждого гоблина любые два его друга враждуют, а любые два врага дружат. Докажите, что для того, чтобы все войско узнало о предстоящем наступлении на Данвин, герцог должен сообщить об этом не менее чем 200 гоблинам.

(Р.~Семизаров)

Задача 3: Обозначим через p(n,k) количество делителей числа n, не меньших, чем k. Чему равна сумма p(1001,1) + p(1002,2) + p(1003,3) +  …  + p(2000,1000)\,?

(С.~Берлов)

Задача 4: BD – биссектриса угла B треугольника ABC. Точка E выбрана так, что  ∠ EAB =  ∠ ACB, AE = DC, и при этом отрезок ED пересекает отрезок AB в точке K. Докажите, что KE = KD.

(С.~Берлов)

Задача 5: Наследство состоит из нескольких бриллиантов и оценивается в 1\,000\,000 долларов. Известно, что его можно разделить на 5, а можно и на 8 равных частей. Какую наибольшую стоимость может иметь самый маленький бриллиант?

Ответ: 50000 (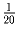 всего наследства).

В качестве примера можно взять по четыре бриллианта стоимостей 50\,000, 75\,000 и 125\,000. Докажем, что наименьший бриллиант не может быть дороже 50\,000. При делении наследства на восемь равных частей по 125\,000 по крайней мере одна часть составлена из двух или более бриллиантов. Заменим каждый бриллиант, стоящий ровно 125\,000, на два бриллианта половинной стоимости – от этого ни стоимость наименьшего бриллианта, ни возможность разбиения на пять частей не изменятся. После этого в каждой части не меньше двух бриллиантов, то есть всего бриллиантов не меньше 16. Значит, при делении на пять частей по 200\,000 в какой-то части окажется по крайней мере четыре бриллианта, и уже в этой части один из бриллиантов стоит не дороже 50\,000.

(Ф.~Назаров)

Задача 6: В вершинах правильного стоугольника произвольным образом расставлены числа от 1 до 100. Разрешается поменять местами два числа, отличающиеся на 1. В результате выполнения таких операций каждое число передвинулось в соседнюю вершину по часовой стрелке. Докажите, что в какой-то момент менялись местами два числа, находившиеся в диаметрально противоположных вершинах.

(М.~Гусаров)

Задача 7: Клетчатый прямоугольник разрезали на прямоугольники 1 × 2 (доминошки) так, что любая прямая, идущая не по линиям сетки параллельно одной из сторон, рассекает четное число доминошек. Докажите, что длина одной из сторон делится на 4.

(Д.~Карпов)