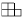Задача 1: Прямоугольник, стороны которого выражаются целыми числами, можно разрезать на фигурки вида [] (сторона клетки на рисунке равна единице). Докажите, что его можно разрезать на прямоугольники 1 × 5 [1 × 3].

(Д.~Карпов)

Задача 2: Решите в вещественных числах систему уравнений

(А.~Храбров)

Задача 3: В ромбе ABCD на сторонах AB и BC взяты, соответственно, точки E и F, такие, что CF/BF = BE/AE = 1994 [1995]. Оказалось, что DE = DF. Найдите величину угла EDF.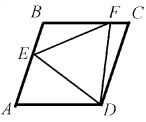

Задача 4: По правилам федерации «Спорт—ЗаРазум» победитель футбольного матча выясняется серией из 129 [130] пар пенальти. Команды пробивают пенальти по очереди. Если одна из команд досрочно обеспечивает себе победу, то пробивание пенальти прекращается, причем решение о прекращении матча принимается в тот момент, когда команды сделали поровну ударов. Сколько голов забила победившая в таком матче команда, если ровно половина всех произведенных ударов попала в ворота?

(А.~Храбров)

Задача 5: Решите уравнение в натуральных числах: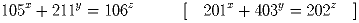

(Д.~Карпов)