 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Отборочный тур >> 9 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1999. Отборочный тур. 9 класс |
|
|
Про вещественные числа x0, x1, …, xn известно, что x0 > x1 > … > xn. Докажите неравенство

(А.~Голованов)
Задача 2:У квадратного трехчлена f(x) = x² + ax + b с целыми коэффициентами значение в 0 по модулю не превосходит 800. Также известно, что f(120) — простое число. Докажите, что у него нет целых корней.
(А.~Храбров)
Задача 3:Для каких n ≥ 3 можно расставить числа от 1 до n в вершинах правильного n-угольника так, чтобы выполнялось следующее свойство: для любых трех вершин A, B и C таких, что AB = AC, число в вершине A либо больше, либо меньше обоих чисел в вершинах B и C?
(С.~Иванов)
Задача 4:На сторонах BC, AC и AB равнобедренного треугольника ABC (AB = BC) выбраны точки A1, B1 и C1. Известно, что ∠ BC1A1 = ∠ CA1B1 = ∠ A. P — точка пересечения отрезков BB1 и CC1. Докажите, что четырехугольник AB1PC1 — вписанный.
(С.Берлов)
Задача 5:Найдите множество значений выражения
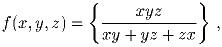
(А.~Храбров)
Задача 6:AL — биссектриса треугольника ABC. Через вершины B и C проведены параллельные прямые b и c, равноудаленные от вершины A. На прямых b и c выбраны точки M и N такие, что отрезки LM и LN пересекаются со сторонами AB и AC соответственно и делятся ими пополам. Докажите, что LM = LN.
(Ф.~Бахарев, С.~Берлов)
Задача 7:Докажите, что число способов разрезать прямоугольник 998 × 999 на
уголки (фигурки вида  не превосходит числа способов разрезать прямоугольник 1998 × 2000 на
уголки так, что никакие два уголка не образуют прямоугольника 2 × 3.
не превосходит числа способов разрезать прямоугольник 1998 × 2000 на
уголки так, что никакие два уголка не образуют прямоугольника 2 × 3.
(Ю.~Белов, А.~Железняк)
Задача 8:Выпуклый n-угольник (n > 3) разбит непересекающимися диагоналями на треугольники. Докажите, что можно отметить n – 1 отрезков из числа проведенных диагоналей и сторон многоугольника так, что никакой набор отмеченных отрезков не образует замкнутую ломаную, и ни из какой вершины не выходит ровно два отмеченных отрезка.
(Д.~Карпов)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1999 >> Отборочный тур >> 9 класс | Показать решения |