 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 10 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2001. Городской тур. 10 класс |
|
|
Квадратные трехчлены f и g с целыми коэффициентами принимают только
положительные значения и  при всех
вещественных x. Докажите, что
при всех
вещественных x. Докажите, что 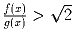 при всех
вещественных x.
при всех
вещественных x.
(А.Храбров)
Задача 2:Компьютер «Intel Пень-V» умеет выполнять с числом только одну операцию: он прибавляет к нему 1, а затем в полученном числе переставляет все нули в конец, а остальные цифры — как угодно (например, из числа 1004 он может получить 1500 или 5100). В компьютер ввели число 12345, и после выполнени 400 операций на экране оказалось число 100000. Сколько раз за это врем на экране компьютера появлялось число, оканчивающееся на ноль?
Задача 3:Точка O — центр вписанной окружности треугольника ABC, точка D — середина стороны AB. Известно, что угол AOD — прямой. Докажите равенство AB + BC = 3AC.
(С.Иванов)
Задача 4:Из таблицы 20 × 20 вырезали прямоугольники 1 × 20, 1 × 19, …, 1 × 1. Докажите, что из оставшейся части таблицы можно вырезать еще 36 прямоугольников 1 × 2.
(С.Берлов)
Задача 5:На биссектрисе AL треугольника ABC выбрана точка K, причем ∠ BKL = ∠ KBL = 30. Прямые AB и CK пересекаютс в точке M, а прямые AC и BK — в точке N. Найдите угол AMN.
(Д.Ширяев, С.Берлов)
Задача 6:Для любых натуральных чисел n > m докажите неравенство
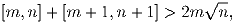
(А.Голованов)
Задача 7:В парламенте страны Альтернативии для любых двух депутатов найдется третий, знакомый ровно с одним из них. Каждый депутат состоит в одной из двух правящих партий. Ежедневно президент приказывает некоторой группе депутатов перейти в другую партию, при этом все депутаты, знакомые хотя бы с одним из депутатов группы, тоже меняют свою партийную принадлежность. Докажите, что президент может добиться того, чтобы все без исключения депутаты Альтернативии перешли в ту партию, которую поддерживает он сам. (Президент не является членом парламента).
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 10 класс | Показать решения |