Задача 1: Существует ли двадцатизначное натуральное число такое, что если его цифры записать в обратном порядке, то полученное число будет ровно в три раза больше первоначального?

(А.Храбров)

Задача 2: Точка D — середина основания AC равнобедренного треугольника ABC. Точка E — основание перпендикуляра, опущенного из точки D на сторону BC. Отрезки AE и BD пересекаются в точке F. Установите, какой из отрезков BF и BE длиннее.

(Ф.Бахарев)

Задача 3: Натуральные числа u и v таковы, что для любого натурального k числа ku + 2 и kv + 3 имеют общий натуральный делитель, больший 1. Чему может быть равно отношение ?

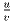
(А.Голованов, Д.Карпов, А.Пастор)

Задача 4:

Задача 5: В треугольнике ABC выполняется равенство BC = 2AC. На стороне BC выбрана такая точка D, что  ∠ CAD =  ∠ CBA. Прямая AD пересекает биссектрису внешнего угла C в точке E. Докажите, что AE = AB.

(С.Берлов)

Задача 6: В некотором государстве 2001 город, причем любые два города соединены прямым рейсом автобуса или поезда. Пользуясь только одним из этих двух видов транспорта невозможно объехать 16 городов, побывав в каждом ровно один раз, и вернуться обратно. Докажите, что пользуясь только одним видом транспорта невозможно объехать 17 городов, побывав в каждом ровно один раз, и вернуться обратно.

(А.Голованов, Д.Карпов)

Задача 7: Колоду карточек с числами от 1 до 78 дают зрителю. Тот ее перемешивает, отбирает 40 карточек, отдает их первому фокуснику, а остальные оставляет себе. Первый фокусник выбирает из полученных карточек две и возвращает их зрителю. Зритель добавляет к этим карточкам одну карточку из своих тридцати восьми, и, перемешав, отдает эти три карточки второму фокуснику. Второй фокусник показывает, какая из карточек была добавлена зрителем. Объясните, как может быть показан такой фокус.
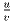