Задача 1:

(Ю.Лифшиц)

Задача 2:

Задача 3: Докажите, что существует бесконечно много натуральных n таких, что наибольший простой делитель числа n⁴ + 1 больше 2n.

Задача 4: Внутри остроугольного треугольника ABC выбираются произвольная точка M такая, что  ∠ AMC +  ∠ ABC = 180. Прямые AM и CM пересекают стороны BC и BA соответственно в точках D и E. Докажите, что описанные окружности треугольника BDE проходит через некоторую фиксированную точку, не зависящую от выбора точки M (отличную от B).

(Ф.Петров)

Задача 5:

Задача 6: Даны вещественные числа x₁, x₂, …, x₁₀ из отрезка [0, π /2], сумма квадратов синусов которых равна 1. Докажите неравенство 3( sin x₁ +  sin x₂ +  …  +  sin x₁₀) ≤  cos x₁ +  cos x₂ +  …  +  cos x₁₀.

Задача 7: Дан выпуклый 2000-угольник M, наибольшее из расстояний между его вершинами равно 1. Известно, что площадь любого выпуклого 2000-угольника, наибольшее из расстояний между вершинами которого равно 1, не превосходит площади многоугольника M. Докажите, что у многоугольника M есть две перпендикулярные диагонали.

(Ф.Бахарев)

Задача 8: Натуральные числа a и b не равны 1. Последовательность x_n задана начальными условиями x₀ = 0 и x₁ = 1 и соотношениями ()

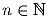
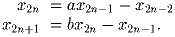
Докажите, что при любых натуральных m и n произведение x_n + m • x_{n + m – 1} •  …  • x_n + 1 делится на x_m • x_m – 1 •  …  • x₁.

(Ю.Певцова)
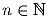