 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Районный тур >> 9 класс >> II вариант | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 2001. Районный тур. 9 класс. II вариант |
|
|
В клетках прямоугольной таблицы 9 × 11 стоят ненулевые цифры. В каждой строчке и в каждом столбце из всех стоящих там цифр составлено многозначное число. Может ли оказаться, что из получившихся 20 чисел ровно одно не делится на 3?
Задача 2:По кругу расставлены 100 положительных чисел (не обязательно целых). Сумма любых 45 чисел, стоящих подряд, равна 250. Докажите, что все расставленные числа не превосходят 30.
Задача 3:Дан остроугольный равнобедренный треугольник ABC (AB = BC). E — точка пересечения перпендикуляра к стороне AB, восставленного в точке B, и прямой AC. D — точка пересечения перпендикуляра к стороне BC, восставленного в точке C, и прямой AB. На перпендикуляре к основанию AC, восставленном в точке A, отметили точку F так, что AF = CD. Докажите, что DE = EF.
Задача 4:Решите систему уравнений в вещественных числах
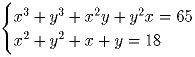
Федя и Кристина стартуют с одного и того же места и равномерно движутся по прямой линии в одном направлении. Федя спокойно идет, а Кристина бежит. Пробежав 500 своих шагов, Кристина поворачивает обратно. В этот момент Федя начинает считать свои шаги и насчитывает до встречи с Кристиной 100 (своих) шага. Чьи шаги длиннее: идущего Феди или бегущей Кристины?
(Ф.Назаров)
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 2001 >> Районный тур >> 9 класс >> II вариант | Показать решения |