 |
 |
|
| Задачная база >> Другие города России >> Челябинские олимпиады >> Внутренняя Челябинская олимпиада >> 11 класс | Показать решения |
|
|
| Другие города России. Челябинские олимпиады. Внутренняя Челябинская олимпиада. 11 класс |
|
|
Задача 2: Найти углы между векторами
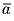 ,
, 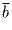 ,
, 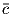 в
пространстве, если известно, что эти углы попарно равны, а
в
пространстве, если известно, что эти углы попарно равны, а 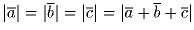 .
.Задача 3: При каком значении параметра a модуль разности корней уравнения x² – 6x + 12 + a² – 4a = 0 принимает наибольшее значение?
Задача 4: Доказать, что для острого угла x и натурального n
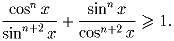
Задача 5: В круге радиуса 1 провели две перпендикулярные хорды AB и CD. Доказать, что |AC|² + |BD|² = 4.
| Задачная база >> Другие города России >> Челябинские олимпиады >> Внутренняя Челябинская олимпиада >> 11 класс | Показать решения |