Задача 1:
Действительные числа a, b, c, x, y, z удовлетворяют
неравенствам:
a² + b² + c² ≤ 6 и x² + y² + z² ≤ 24. Докажите, что
a) ax + by + cz ≤ 15
b) ax + by + cz ≤ 12.
Задача 2:
На плоскости задано 2N точек. Два игрока играют в следующую игру:
каждый из них в свою очередь хода выбирает точку из числа еще не
выбранных. После того, как все точки разобраны, каждый из игроков
подсчитывает сумму попарных расстояний между N выбранными им точками.
Побеждает тот игрок, у которого эта сумма меньше. Докажите, что
при правильной игре начинающий не проиграет.
Задача 3:
Kаждая сторона треугольника
разделена на 3 равные части,
и проведены прямые, как указано на рисунке. Во сколько раз площадь
заштрихованного треугольника меньше площади исходного?
Задача 4:
Вася выписывает в тетрадку натуральные числа N
1, N
2, … ,
N
k, N
k + 1, … по следующему правилу: N
1 выбирается
произвольно, а N
i + 1 равно увеличенному на 3000 остатку от деления
числа
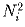
на 1996. Докажите, что всегда найдется бесконечное
множество равных между собой чисел

номера которых образуют возрастающую
арифметическую прогрессию.


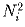 на 1996. Докажите, что всегда найдется бесконечное
множество равных между собой чисел
на 1996. Докажите, что всегда найдется бесконечное
множество равных между собой чисел  номера которых образуют возрастающую
арифметическую прогрессию.
номера которых образуют возрастающую
арифметическую прогрессию.