Задача 1:
Доказать, что для всех натуральных n выполнено неравенство:
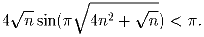
Задача 2:
Какое наименьшее число круглых фишек диаметром
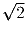
можно
расставить на доске 7 × 7 клеток так, чтобы внутри каждой
клетки хотя бы одна точка была покрыта некоторой фишкой?
(Длина стороны клетки равна 1).
Задача 3:
Решите в целых числах уравнение: y³ = x
6 + 2x
4 – 1000.
Задача 4:
В единичном кубе (рис.3) пропилены 3 сквозных отверстия в форме
прямоугольных параллелепипедов, основаниями которых являются квадраты
(рис.4) с диагоналями, расположенными на средних линиях граней.
Диагонали квадратов равны ½. Определите объем «дырявого»
куба.


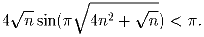
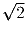 можно
расставить на доске 7 × 7 клеток так, чтобы внутри каждой
клетки хотя бы одна точка была покрыта некоторой фишкой?
(Длина стороны клетки равна 1).
можно
расставить на доске 7 × 7 клеток так, чтобы внутри каждой
клетки хотя бы одна точка была покрыта некоторой фишкой?
(Длина стороны клетки равна 1).