Задача 1:
Действительные числа x, y и z удовлетворяют системе
неравенств:
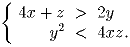
Докажите, что z > 0.
Задача 2:
Требуется разрезать квадратный торт на n (n ≥ 6) квадратных
кусков (не обязательно одинаковых). Для каких n это возможно?
Задача 3:
На горизонтальной поверхности лежат в ряд, касаясь друг друга,
100 одинаковых бревен, сплошь вымазанных дегтем. В ложбину между двумя
самыми левыми бревнами кладут такое же, но чистое бревно и без
проскальзывания катят его вправо до самой правой ложбины. Какая часть
боковой поверхности этого бревна останется чистой к концу пути?
Задача 4:
Пусть p – простое число, большее 3. Известно, что для некоторого
натурального n запись числа p
n содержит ровно 20 цифр. Докажите,
что среди них найдутся 3 одинаковые цифры.