Задача 1:
Докажите, что для любых положительных чисел x, y, и z
выполняется неравенство:
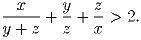
Задача 2:
Дан треугольник ABC, в котором AB = BC. На стороне AB выбрана
точка E, а на продолжении стороны AC за точку A – точка D
так, что ∠ BDC = ∠ ECA. Докажите, что площади треугольников
DEC и ABC равны.
Задача 3:
Найдите все натуральные числа n, при которых дробь
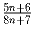
сократима.
Задача 4:
В так-тиль играют вдвоем на
доске 4 × 4 восемью шашками двух
цветов. Начальное расположение шашек указано на рисунке. Игроки ходят
по очереди, начинают игру белые. Ход заключается в перестановке шашки
своего цвета на соседнее по вертикали или по горизонтали (но
не по диагонали) свободное поле.
Побеждает игрок, первым выстроивший ряд из
трех своих шашек (по горизонтали, вертикали или диагонали). Двое
школьников не успели доиграть на уроке партию и отложили ее.
Вернувшись с перемены, они напрочь забыли, чей ход в отложенной
позиции. Всегда ли они смогут восстановить очередность хода?


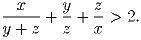
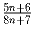 сократима.
сократима.