Задача 1:
N пятаков (N ≥ 5) лежат гербами вверх. За один ход
разрешается перевернуть любые N – 1 пятаков. Для каких N
можно за несколько шагов добиться того, чтобы все пятаки легли
гербами вниз?
Задача 2:
Можно ли в таблицу N × (N – 1) вписать натуральные числа так, чтобы
сумма чисел в каждой строке имела вид
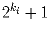
, а в каждом
столбце – 14m
j + 5, где k
i и m
j – некоторые натуральные
числа.
Задача 3:
Найти все значения параметра a, при которых неравенство
x² + 5|x + a| ≥ a²
справедливо для любого x.
Задача 4:
Назовем пузатостью прямоугольника отношение длины меньшей стороны
к длине большей стороны. Разрежем квадрат произвольным образом на
конечное число прямоугольников, стороны которых параллельны сторонам
квадрата. Докажите, что сумма пузатостей всех прямоугольников не меньше 1.


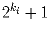 , а в каждом
столбце – 14mj + 5, где ki и mj – некоторые натуральные
числа.
, а в каждом
столбце – 14mj + 5, где ki и mj – некоторые натуральные
числа.