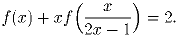Задача 1:
Найдите функцию f, определенную на всей числовой прямой
и при всех x ≠ ½ удовлетворяющую уравнению:
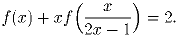
Задача 2:
Точка K делит сторону BC треугольника ABC в отношении
p:q, считая от вершины B.
Точка F делит сторону AC в отношении α : β ,
считая от вершины A. В каком отношении
прямая BF делит отрезок AK?
Задача 3:
Натуральные числа n, m и k (n < m < k) являются длинами
сторон треугольника, один из углов которого равен 120°.
Какое наименьшее значение может принимать n ?
Задача 4:
На чемпионате мира по футболу 1994 года по окончании
групповых игр (в группе 4 команды) очки,
набранные командами одной из групп, образовали
арифметическую прогрессию с разностью, отличной от нуля.
Сколько очков набрала команда, занявшая третье место в этой
группе?
Примечание: игры в группах проводились в один круг, победитель
каждого матча получал 3 очка, проигравший – 0, а в случае
ничьей каждая команда получала по 1 очку.