Задача 1: Определённая на всей числовой прямой функция f(x) такова,
что выполнено тождество:
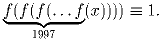
Какое наименьшее количество корней может иметь уравнение f(x) = 1?
Задача 2: Рассматриваются все натуральные числа n такие,
что числа n + 1 и 2n + 1 – точные квадраты. Найдите наибольший
общий делитель всех рассматриваемых чисел.
Задача 3: Пусть A1A2 … A105 – правильный 105-угольник,
O – центр вписанной в него окружности. Рассматриваются
все вектора 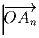 , где номер вершины
n взаимно прост с числом 105 (натуральные числа называются взаимно
простыми, если они не имеют общих делителей, отличных от 1).
Найдите сумму всех рассматриваемых векторов.
, где номер вершины
n взаимно прост с числом 105 (натуральные числа называются взаимно
простыми, если они не имеют общих делителей, отличных от 1).
Найдите сумму всех рассматриваемых векторов.
((Предложена Стасом Васильевым.))
Задача 4: Торт имеет форму произвольного треугольника.
Двое сластен делят его следующим образом. Первый указывает
на торте точку, второй проводит через эту точку прямолинейный разрез
и забирает себе большую часть. Какую наибольшую часть
торта может обеспечить себе первый сластена? Считается, что торт всюду имеет
одинаковую толщину.
((Предложена В.Т.Шевалдиным.))


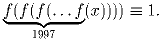
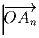 , где номер вершины
n взаимно прост с числом 105 (натуральные числа называются взаимно
простыми, если они не имеют общих делителей, отличных от 1).
Найдите сумму всех рассматриваемых векторов.
, где номер вершины
n взаимно прост с числом 105 (натуральные числа называются взаимно
простыми, если они не имеют общих делителей, отличных от 1).
Найдите сумму всех рассматриваемых векторов.