 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 11 класс >> 1-й день | Показать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 11 класс. 1-й день |
|
|
Докажите, что для любого натурального числа n справедливо двойное неравенство:
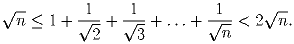
(Предложена С.А.Аникиным.)
Задача 2:Пусть a1,a2, … ,an, … – произвольная последовательность вещественных чисел. Для натурального n обозначим через fn(x) функцию fn(x) = sin (2nx – an).
а) Докажите, что для любого натурального k найдётся такое число x, что все числа f1(x),f2(x), … ,fk(x) положительны.
б) верно ли аналогичное утверждение, если вместо fn(x) рассматривать функции gn(x) = sin (nx – an)?
(Предложена М.Ф.Прохоровой.)
Задача 3:По окружности на равном расстоянии друг от друга расставлено 2n корзин с яблоками, причём число яблок в любых двух соседних корзинах отличается ровно на 1. При каких натуральных n можно гарантировать, что найдутся две диаметрально противоположные корзины, содержащие поровну яблок?
(Предложена С.Э.Нохриным.)
Задача 4:Дан выпуклый четырёхгранный угол. Всегда ли найдётся плоскость, сечение которой данного угла является параллелограммом?
((Предложена В.В.Нагребецким.))
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 11 класс >> 1-й день | Показать решения |