 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 8 класс >> 2-й день | Показать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 8 класс. 2-й день |
|
|
Корни квадратного уравнения x² + ax + 1 = b – целые, отличные от нуля числа. Докажите, что число a² + b² составное.
(Взята из журнала ``Квант" за 1970 год.)
Задача 2:Найдите все натуральные числа, представимые в виде
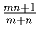 , где m и n – натуральные числа.
, где m и n – натуральные числа.
(Рекомендована жюри Российской олимпиады.)
Задача 3:На автобусном маршруте 11 остановок, включая первую. На первой остановке в автобус село 10 пассажиров, и на каждой последующей остановке, кроме конечной, суммарное количество вошедших и вышедших пассажиров было равно 10. Кроме того оказалось, что каждый пассажир ехал не более 5 остановок (то есть от остановки с номером M не далее, чем до остановки с номером M + 5), и ни в какой момент автобус не был пустым. Какое наибольшее количество пассажиров могло одновременно оказаться в автобусе во время движения?
(Рекомендована жюри Российской олимпиады.)
Задача 4:Медианой пятиугольника ABCDE назовём отрезок, соединяющий вершину с серединой противоположной стороны (A – с серединой CD, B – с серединой DE и т.д.). Докажите, что если 4 медианы выпуклого пятиугольника перпендикулярны сторонам, к которым они проведены, то таким же свойством обладает и пятая медиана.
(Рекомендована жюри Российской олимпиады.)
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 8 класс >> 2-й день | Показать решения |