 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 9 класс >> 2-й день | Показать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 9 класс. 2-й день |
|
|
Можно ли расставить числа от 0 до 9 в кружочках (см. рисунок) так, чтобы сумма трех чисел по любому из отрезков была одной и той же?
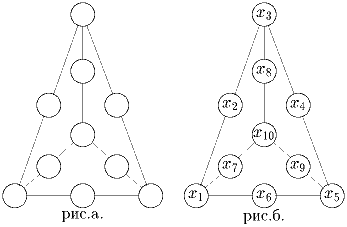
(Рекомендована жюри Российской олимпиады.)
Задача 3:Дана полоска клетчатой бумаги длиной в 100 клеток. Двое играющих по очереди красят клетки в чёрный цвет, причём первый всегда красит 4 подряд стоящие клетки, а второй – три подряд стоящие. Уже покрашенную клетку вторично раскрашивать нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выиграет при наилучшей игре с обеих сторон?
(Рекомендована жюри Российской олимпиады.)
Задача 4:На прямой заданы последовательно точки B,L,C,F так, что
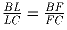 .
Через точки L и F проведена окружность так, что LF – диаметр.
Пусть A произвольная точка окружности, не лежащая на прямой.
Доказать, что AL – биссектриса угла ∠ BAC.
.
Через точки L и F проведена окружность так, что LF – диаметр.
Пусть A произвольная точка окружности, не лежащая на прямой.
Доказать, что AL – биссектриса угла ∠ BAC.
(Предложена В.Н.Ушаковым.)
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 9 класс >> 2-й день | Показать решения |