Задача 1:
Докажите, что для любых неотрицательных чисел a, b и c
справедливо неравенство:
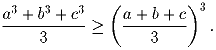
Задача 2:
Покажите, что уравнение x³ + x = y²
не имеет целочисленных решений кроме x = y = 0.
Задача 3:
На окружности даны 20 точек. Двое по очереди проводят хорды с
концами в этих точках так, чтобы хорды не пересекались. Проигрывает тот,
кто не сможет провести хорду. Кто победит при правильной игре –
начинающий, или его партнёр?
Задача 4:
Используя неравенство
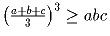
,
справедливое для любых положительных чисел a, b и c, докажите,
что из всех треугольников с данным периметром наибольшую площадь
имеет правильный треугольник.


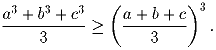
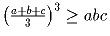 ,
справедливое для любых положительных чисел a, b и c, докажите,
что из всех треугольников с данным периметром наибольшую площадь
имеет правильный треугольник.
,
справедливое для любых положительных чисел a, b и c, докажите,
что из всех треугольников с данным периметром наибольшую площадь
имеет правильный треугольник.