 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Заочный тур >> 10 класс | Показать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Заочный тур. 10 класс |
|
|
Над планетой, имеющей форму шара, летают три спутника. Докажите, что в любой момент времени на поверхности планеты имеется точка, из которой ни один из спутников не виден. Спутники считаются точечными.
Проведём плоскость через 3 точки – спутника, и восстановим к ней перпендикуляр из центра планеты. Пусть он пересекает поверхность планеты в точках A и B, а проведённую плоскость в точке C. Тогда если AC ≥ BC, то из точки A не видна вся проведённая плоскость, а поэтому и все спутники. Если же AC < BC, то таким свойством обладает точка B.
Задача 3: Докажите, что уравнение m! • n! = k! имеет бесконечно много решений таких, что n, m и k – натуральные числа, большие 1. Задача 4:Изобразите на плоскости AOB множество пар (a;b), таких что ситема уравнений
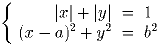
а) имеет ровно 8 решений;
б) имеет ровно 7 решений;
в) не имеет решений;
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Заочный тур >> 10 класс | Показать решения |