Задача 5:
Пусть фиксированы положительные числа m и M такие, что m < M. Пусть
также m ≤ x
j ≤ M,j = 1,\,2,\, … ,\,n. Рассматривается
следующая задача: найти наибольшее
значение выражения
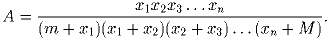
Х.Гюйгенс доказал, что решение этой задачи существует, и нашёл
единственные числа
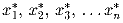
из отрезка
[m,M], при которых выражение A
принимает наибольшее значение. Сможете ли Вы найти эти числа?
Задача 6:
Докажите, что уравнение x² + y² = z³ имеет бесконечно много решений в
натуральных числах.
Задача 7:
Ортогональные проекции на плоскости всех граней треугольной пирамиды
отрезка, соединяющего
середины его противоположных рёбер, имеют равные длины. Докажите, что таким
же свойством обладает и любой из двух других отрезков, соединяющих
середины противоположных рёбер пирамиды.
(Н.Агаханов)
Задача 8:
Есть три поля: на одном лежит стопка из n монет, два других свободны.
За один ход можно переложить монету с верха любой стопки на свободное
поле или на верх любой другой стопки. За какое наименьшее число ходов
удастся собрать стопку в обратном порядке на том же поле?
(А.Шаповалов)


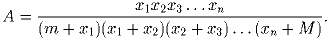
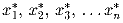 из отрезка
[m,M], при которых выражение A
принимает наибольшее значение. Сможете ли Вы найти эти числа?
из отрезка
[m,M], при которых выражение A
принимает наибольшее значение. Сможете ли Вы найти эти числа?