 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 8 класс >> 2-й день | Показать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 8 класс. 2-й день |
|
|
(А.Шаповалов)
Задача 6: Проверьте следующее равенство: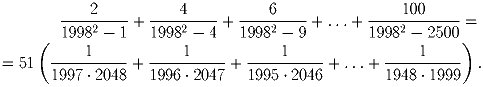
Задача 7: В треугольнике ABC проведены биссектрисы AA1 и CC1. Докажите, что если длины перпендикуляров, опущенных из вершины B на прямые AA1 и CC1 равны, то треугольник ABC — равнобедренный.
(Н.Агаханов)
Задача 8: Прожектор освещает развёрнутый угол (180). Можно ли расположить 19 прожекторов так, чтобы никакие 3 из них не находились на одной прямой и каждый прожектор освещал бы только один другой прожектор?
(Т.Емельянова)
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 8 класс >> 2-й день | Показать решения |