Задача 1:
Пусть M – точка внутри квадрата
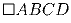
, причем
∠ BAM = 30, и ∠ BCM = 15.
Найти ∠ MDA.
Задача 2:
Пусть числа a,b,c удовлетворяют неравенствам
a + b + c > 0,ab + ac + bc > 0,abc > 0.
Доказать, что a > 0,b > 0,c > 0.
Задача 3:
Натуральные числа a,b,c таковы, что a² + b² + c²
делится на ab + bc + ca, а число
a + b + c – простое.
Докажите, что a = b = c = 1.
Задача 4:
15 команд играют турнир в один круг.
Докажите, что в некотором матче встретятся команды, сыгравшие
перед этим в сумме нечетное число матчей.


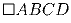 , причем
∠ BAM = 30, и ∠ BCM = 15.
Найти ∠ MDA.
, причем
∠ BAM = 30, и ∠ BCM = 15.
Найти ∠ MDA.