 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 11 класс | Показать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Заочный тур. 11 класс |
|
|
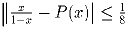 для всех x ∈ [0;½].
для всех x ∈ [0;½].Задача 2: Натуральные числа M и K отличаются перестановкой цифр. Доказать, что
а) сумма цифр чисел 2M и 2K одинакова;
б) сумма цифр чисел 5M и 5K одинакова.
Задача 3: Каково наибольшее возможное число вершин многоугольника, все стороны которого лежат на 6 прямых?
Задача 4: Существуют ли такие 100 треугольников, ни один из которых нельзя покрыть 99 остальными?
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 11 класс | Показать решения |