Задача 1: Доказать, что для всех действительных чисел a справедливо неравенство: 3(1 + a² + a⁴) ≥ (1 + a + a²)².

Задача 2: Пусть числа 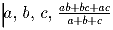 – целые. Докажите, что число 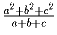 – целое.

Задача 3: Пусть 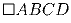 — квадрат. M — внутренняя точка квадрата. Доказать, что точки пересечения медиан треугольников  ∆ AMB,  ∆ BMC,  ∆ CMD,  ∆ DMA тоже образуют квадрат.

Задача 4: Можно ли расставить в вершинах куба различные числа так, чтобы каждое число равнялось сумме трех, соединенных с ним ребрами куба?

Решение. Обозначим числа в в вершинах куба через a, b, c, d, f, k, l, m. Тогда

a = b + d + f

b = a + c + k

c = b + d + l

d = a + c + m

f = a + k + m

k = b + f + l

l = c + k + m

m = d + l + f

Сложив почленно эти равенства имеем: a + b + c + d + f + k + l + m = 3(a + b + c + d + f + k + l + m), откуда a + b + c + d + f + k + l + m = 0. Но a + b + c + d + f + k + l + m = a + (b + d + f) + l + (c + k + m) = 2a + 2l, откуда a =  – l. Аналогично доказывается, что b =  – m, c =  – f, d =  – k (*).

Отсюда получаем способ расстановки чисел: например, b = 1 d = 2 f = 3. Тогда по условию a = b + d + f = 6, а остальные числа находим из условия (*): l =  – 6, c =  – 3, m =  – 1, k =  – 2.

Ответ: можно.