 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 9 класс | Показать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Заочный тур. 9 класс |
|
|
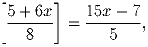
Задача 2: Число A вида 100 … 01 кратно 19.
Докажите, что A кратно 13.
Задача 3: Треугольники ∆ ABC и ∆ OBC оба равносторонние. Точка M лежит на окружности с центром O и радиусом OB.
Докажите, что MB² + MC² = MA².
Задача 4: Все натуральные числа поделены на хорошие и плохие. Известно, что если n – хорошее, то и число n + 6 – хорошее, а если число m – плохое, то и число m + 15 – плохое.
Может ли среди первых 2000 чисел быть ровно 1000 хороших?
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Заочный тур >> 9 класс | Показать решения |