Задача 1:
Верно ли, что существует натуральное число M,
обладающее свойством: все натуральные числа, большие M,
представимы в виде суммы квадрата и куба каких-то двух натуральных чисел?
Задача 2:
Первой точкой Брокара в треугольнике ABC называется такая точка
P, что ∠ PAC = ∠ PCB = ∠ PBA.
Из точки P опущены перпендикуляры
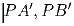
и
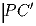
на стороны BC, CA и AB соответственно. Докажите, что
а) треугольники ∆ ABC и 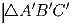 подобны;
подобны;
б) коэффициент их подобия равен 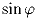 , где
, где 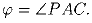
Задача 3:
Числа a, b и c удовлетворяют равенствам:
ab + bc + ac = 1999abc, и 1999(a + b + c) = 1. Найти a
1999 + b
1999 + c
1999.
Задача 4:
Пусть a
1, a
2, … , a
n — целые числа такие, что все числа
b
1, b
2, … ,b
n (b
i равно произведению цифр числа a
i)
различны и не равны нулю. Верно ли, что сумма
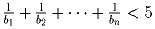
?


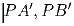 и
и 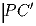 на стороны BC, CA и AB соответственно. Докажите, что
на стороны BC, CA и AB соответственно. Докажите, что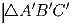 подобны;
подобны;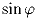 , где
, где 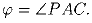
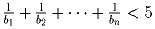 ?
?