Задача 1:
В чемпионате школы по футболу участвуют N команд.
Игры проводятся в один
круг, за победу команде даётся 3 очка, за ничью — 1 очко, за
поражение — 0 очков.
Команда «Mатематики" торопилась на олимпиаду по математике,
поэтому провела все свои матчи досрочно. После этого команда
знала, что независимо от результатов оставшихся
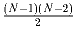
матчей, она займёт место не ниже k-го (1 ≤ k ≤ N).
Какое наименьшее число очков могло быть у команды «Математики"?
Задача 2:
Про квадратные трехчлены f
1, f
2 и f
3
с разными старшими коэффициентами
известно, что их разности
f
1 – f
2, f
2 – f
3 и f
3 – f
1 имеют по одному корню.
Докажите, что эти корни совпадают.
Задача 3:
Пусть M — точка на диаметре AB окружности с центром в точке
O; C и D — точки окружности, расположенные по одну сторону
от AB и такие, что ∠ CMA = ∠ DMB, ∠ OCM = α .
Чему равен угол ∠ ODM?
Задача 4:
Каково наибольшее число подряд идущих членов последовательности
x
n = n² + 1999, наибольший общий делитель которых больше 1?


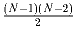 матчей, она займёт место не ниже k-го (1 ≤ k ≤ N).
Какое наименьшее число очков могло быть у команды «Математики"?
матчей, она займёт место не ниже k-го (1 ≤ k ≤ N).
Какое наименьшее число очков могло быть у команды «Математики"?