Задача 1: Король приказал чеканить монеты. Порядок выпуска монет был определен так. Сначала чеканятся монеты в наименьшую возможную сумму — 1 крона. Затем на каждом следующем шаге казначей определяет наименьшую целочисленную сумму, которую нельзя набрать десятью или меньшим числом уже отчеканенных монет, и выпускаются монеты достоинством в эту сумму. Какие монеты будут выпущены в королевстве?

Задача 2: Решите систему уравнений в натуральных числах n и m:

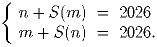
Здесь через S(k) обозначается сумма цифр натурального числа k.

Задача 3: Бумажный треугольник ABC перегнули по прямой, в результате чего вершина C попала на сторону AB, а непокрытая часть разбилась на два равнобедренных треугольника, у которых равные стороны сходятся в вершинах A и B. Найдите угол C.

Задача 4: Барон Мюнгхаузен утверждает, что он придумал такое натуральное число, что для любых натуральных чисел n и k, не больших 1999, это число можно представить в виде произведения n различных натуральных чисел, являющихся точными k-ми степенями. Может ли утверждение барона быть истинным?