Задача 1:
Доказать неравенство
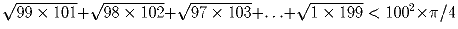
Задача 2:
64 кубика уложили в квадрат 8 × 8. Можно ли эти же
кубики уложить в виде куба 4 × 4 × 4 таким образом, чтобы
кубики бывшие соседними, соседними и оставались?
Задача 3:
Решить уравнение:
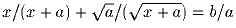 Задача 4:
Задача 4:
В прямоугольном треугольнике построена окружность, которая
касается двух других сторон и описанной окружности. Что больше ее
радиус или диаметр вписанной окружности?
Задача 5:
На доске N точек общего положения, т.е. никакие три из них не
лежат на одной прямой. Каждый из трех играющих игроков соединяет
отрезком две точки. Построенные отрезки не могут пересекаться ни
в каких внутренних точках. Выигрывает тот, кто сделает последний
ход. В результате одной игры выиграл первый. Мог ли исход быть
иным при другой игре второго и третьего игроков?


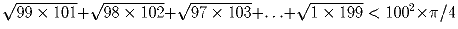
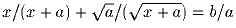 Задача 4:
В прямоугольном треугольнике построена окружность, которая
касается двух других сторон и описанной окружности. Что больше ее
радиус или диаметр вписанной окружности?
Задача 4:
В прямоугольном треугольнике построена окружность, которая
касается двух других сторон и описанной окружности. Что больше ее
радиус или диаметр вписанной окружности?