Задача 1:
(5б) Найдется ли натуральное число n такое, что n
6 – 5n
4 + 3n² + 1
делится на 399?
Задача 2:
(4б) Решить систему уравнений
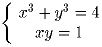
Задача 3:
(4б) Некоторая фигура проектируется на две взаимно
перпендикулярные плоскости. Если ее проекциями
являются два равносторонних треугольника, то могут ли
они быть разными?
Задача 4:
(4б) Доказать, что последние цифры чисел
1 • 2/2, 2 • 3/2, 3 • 4/2, …, n*(n + 1)/2, …
периодически повторяются.
Задача 5:
(4б) Периметр данного параллелепипеда ABCD, AB < BC, равен 26 см,
а угол ABC равен 120 градусов. Радиус окружности, вписанной в
треугольник BCD, равен
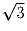
см. Найти стороны параллелограмма.


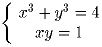
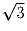 см. Найти стороны параллелограмма.
см. Найти стороны параллелограмма.