 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 10 класс | Показать решения |
|
|
| XXV всероссийская математическая олимпиада школьников. Заключительный этап. 10 класс |
|
|
На столе стоят три пустых банки из-под меда. Винни-Пух, Кролик и Пятачок по очереди кладут по одному ореху в одну из банок. Их порядковые номера до начала игры определяются жребием. При этом Винни может добавлять орех только в первую или вторую банку, Кролик – только во вторую или третью, а Пятачок – в первую или третью. Тот, после чьего хода в какой-нибудь банке оказалось ровно 1999 орехов, проигрывает. Докажите, что Винни-Пух и Пятачок могут, договорившись, играть так, чтобы Кролик проиграл.
Задача 2:
Найдите все бесконечные ограниченные
последовательности натуральных чисел a1, a2, a3, …,
для всех членов которых, начиная с третьего, выполнено
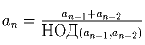 .
.
Пусть окружность, вписанная в треугольник ABC, касается его сторон AB, BC и AC в точках K, L и M соответственно. К окружностям, вписанным в треугольники BKL, CLM и AKM, проведены попарно общие внешние касательные, отличные от сторон треугольника ABC. Докажите, что эти касательные пересекаются в одной точке.
Задача 4:
В квадрате n × n клеток бесконечной шахматной доски расположены n² фишек, по одной фишке в каждой клетке. Ходом называется перепрыгивание любой фишкой через соседнюю по стороне фишку, непосредственно за которой следует свободная клетка. При этом фишка, через которую перепрыгнули, с доски снимается. Докажите, что позиция, в которой дальнейшие ходы невозможны, возникнет не ранее, чем через [n²/3] ходов.
Задача 5:
Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800. Чему равна сумма цифр числа 3n?
Задача 6:В треугольнике ABC окружность, проходящая через вершины A и B, касается прямой BC, а окружность, проходящая через вершины B и C, касается прямой AB и пересекает первую окружность в точке K, K ≠ B. Пусть O – центр описанной окружности треугольника ABC. Докажите, что угол BKO – прямой.
Задача 7:Для некоторых положительных чисел x и y выполняется неравенство x² + y³ ≥ x³ + y4. Докажите, что x³ + y³ ≤ 2.
Задача 8:В некоторой группе из 12 человек среди каждых 9 найдутся 5 попарно знакомых. Докажите, что в этой группе найдутся 6 попарно знакомых.
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 10 класс | Показать решения |