 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Командная олимпиада >> Младшая группа | Показать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Командная олимпиада. Младшая группа |
|
|
Дробная часть квадрата рационального числа r равна 1/4. Докажите, что число 2r – целое.
Задача 2:Найдите все натуральные n, для которых существуют два подряд идущих натуральных числа, суммы цифр которых делятся на n.
Задача 3:Если расположить 2000 отрезков в виде 2000-угольника, то их концами будут ровно 2000 точек. А сколько еще разных концов может быть у 2000 различных отрезков? Перечислите все возможности, приведите соответствующие примеры и докажите, что других возможностей нет.
Задача 4:Прямая касается вписанной окружности равностороннего треугольника ABC и пересекает его стороны AB и AC в точках D и E соответственно. Докажите, что
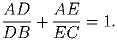
Задача 5:
На клетчатой доске размером 1000 × 1000 стоят красные, синие и зеленые фишки (в каждой клетке – не больше одной фишки). Рядом (в соседних по стороне клетках) с любой красной фишкой стоят 2 синие, а рядом с любой синей – 3 зеленые. Докажите, что есть зеленая фишка, рядом с которой нет красных.
Задача 6:
Внутри данного треугольника ABC выбрана такая точка P, что угол PBC равен углу PCA. Прямая BP пересекает описанную окружность треугольника ABC в точке E ≠ B. Описанная окружность треугольника APE пересекает продолжение отрезка CE за точку E в точке F. Докажите, что отношение площади треугольника ABP к площади четырехугольника APEF не зависит от выбора точки P.
Задача 7:Граф G связен. Назовем разрезом минимальное по включению множество вершин, при удалении которых (вместе со всеми выходящими из них ребрами) граф теряет связность. Известно, что при удалении вершин разреза R вершины из разреза S оказываются в одной компоненте связности. Докажите, что при удалении вершин разреза S вершины из разреза R оказываются в одной компоненте связности.
Задача 8:
a1, …, an – положительные числа, меньшие 1. Докажите, что
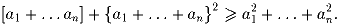
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Командная олимпиада >> Младшая группа | Показать решения |