 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 2-й тур >> Первая лига | Показать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Турнир матбоёв. 2-й тур. Первая лига |
|
|
На множестве целых чисел определена операция *. Известно, что для любых целых a,b,c выполняются следующие условия:
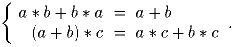
Найдите 2000*2067.
Задача 2:
С рядом из нулей и единиц разрешается проделывать такую операцию: несколько (может быть, ни одного) идущих подряд с начала последовательности нулей заменить на единицы, а следующий за ними знак заменить на противоположный (1 на 0, а 0 на 1). За какое наименьшее количество таких операций из 20 единиц можно получить одни нули?
Задача 3:
В некотором государстве 4nаэропортов, из каждого аэропорта выходит ровно 3 авиалинии (авиалиния соединяет два аэропорта). Из любого аэропорта можно долететь до любого другого (возможно, с пересадками). Пусть K – количество способов продать все авиалинии трем авиакомпаниям таким образом, чтобы из каждого аэропорта выходили три авиалинии разных авиакомпаний. Докажите, что K ≤ 3 • 2³n.
Задача 4:
Про натуральные числа x, y и z известно, что (z + 1)x² + x = zy² + y. Докажите, что y – x является точным квадратом.
Задача 5:
Докажите, что отношение периметра описанного четырехугольника к
сумме его диагоналей не меньше, чем 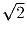 .
.
Задача 6:
Найдите все такие многочлены P(x) с целыми коэффициентами, что P(n – 1) + P(n + 1) делится на P(n) для бесконечного множества натуральных n.
Задача 7:
Двое играют в крестики-нолики на бесконечной клетчатой полосе ширины 1. Первый ходит одним крестиком, второй – сотней ноликов (не обязательно подряд). Цель первого – получить три крестика, один из которых стоит точно посередине между двумя другими, цель второго – помешать первому это сделать. Докажите, что первый может выиграть за 40 ходов, как бы ни играл второй.
Задача 8:
Дан пятиугольник ABCDE в котором AB = BC и ∠ A = ∠ C = 90. Точка Fна
стороне ED такова, что 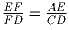 . Докажите,
что ∠ ACF = ∠ ABE.
. Докажите,
что ∠ ACF = ∠ ABE.
Задача 9:
Из каждой вершины (не обязательно выпуклого) многоугольника можно провести диагональ длины, не превосходящей 1, целиком лежащую внутри многоугольника. Докажите, что у этого многоугольника найдется сторона, длина которой не превосходит 1.
Задача 10:
Пусть n ≥ 2 – натуральное число. Докажите, что
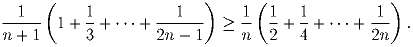
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 2-й тур >> Первая лига | Показать решения |