Задача 1:
Задача 2:
Задача 3:
Задача 4:
Задача 5:
Найдите все непрерывные функции
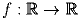
,
которые удовлетворяют неравенствам f(2x) – f(x) ≥ 3x² + x и
f(3x) – f(x) ≤ 8x² + 2x при каждом
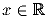
.
Задача 6:
Задача 7:
Окружности S
1, S
2 и S
3 пересекаются в точке A.
Кроме того, первые две окружности пересекаются в точке B,
первая и третья – в точке C, а вторая и третья – в точке D.
Касательные к окружности S
2 в точке B и к окружности S
3 в точке
C пересекаются на окружности S
1. Докажите, что касательные к
окружности S
2 в точке D и к окружности S
1 в точке C
пересекаются на окружности S
3.
Задача 8:
Числа 1, …, p – 1 разбиты на три непустых множества.
Докажите, что если число p – простое,
то можно выбрать по одному числу из каждой группы так, чтобы сумма
каких-то двух выбранных чисел была сравнима с третьим по модулю p.


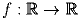 ,
которые удовлетворяют неравенствам f(2x) – f(x) ≥ 3x² + x и
f(3x) – f(x) ≤ 8x² + 2x при каждом
,
которые удовлетворяют неравенствам f(2x) – f(x) ≥ 3x² + x и
f(3x) – f(x) ≤ 8x² + 2x при каждом 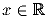 .
Задача 6:
.
Задача 6: