Задача 1: Изобразите на координатной плоскости множество точек (x,y), для которых

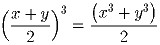
Задача 2: В клетках квадратной таблицы 3 × 3 расставлены числа 1, 2, 3, …, 9 так, что сумма каждых четырех чисел, заполняющих квадрат 2 × 2, равна одному и тому же числу S. Найдите все возможные значения S.

Задача 3: Докажите, что существуют различные стозначные числа A и B, являющиеся точными кубами, что цифры десятичной записи числа A, записанные в обратном порядке, образуют число B.

Задача 4: В выпуклом четырехугольнике проведены биссектрисы всех его углов. Может ли каждая из сторон четырехугольника пересекаться какой-либо биссектрисой в точке, отличной от вершины?

Задача 5: Рассматриваются все трехчлены вида ax² + bx + c с натуральными коэффициентами, не превосходящими 100. Каких трехчленов больше: имеющих действительные корни или не имеющих?

Задача 6: Сторона BC треугольника ABC разбита точками M и N на три равные части (BM = MN = NC); K и L – середины сторон AB и AC соответственно. Прямая LM пересекает прямую AB в точке E, прямая KN пересекает прямую AC в точке F. Докажите, что прямая EF параллельна прямой BC.

Задача 7: Найдите все натуральные n, которые равны сумме некоторых трех различных натуральных делителей числа n – 1.

Задача 8: У нас есть куча монет. Известно, что настоящих среди них больше, чем фальшивых, все настоящие монеты весят одинаково. Любая фальшивая монета отличается по весу от настоящей, но фальшивые монеты могут иметь разный вес. Мы можем пользоваться чашечными весами, владелец которых после каждого взвешивания забирает себе (в качестве нашей платы) любую выбранную им монету из взвешенных. Докажите, что можно выделить хотя бы одну настоящую монету, которая останется у нас.