Задача 1:
Последовательность a
n задана условиями a
1 = 1,
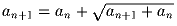
при всех n ≥ 1. Найдите
a
1998.
Задача 2:
Внутри выпуклого пятиугольника ABCDE взята точка M. Может ли
оказаться, что каждая из прямых MA, MB, MC, MD, ME отсекает
от пятиугольника ABCDE треугольник?
Задача 3:
Сергей Геннадьевич, взяв менее 100 рублей, пошел гулять. Заходя в
какое-либо кафе и имея при этом m рублей n копеек, он тратил
n рублей m копеек. Какое наибольшее число кафе мог посетить
Сергей Геннадьевич?
Задача 4:
AD и BC – основания равнобедренной трапеции ABCD, O –
точка пересечения ее диагоналей. Докажите, что окружности,
описанные около треугольников ABO и COD пересекаются в центре
окружности, описанной около трапеции ABCD.
Задача 5:
На поверхности куба проведена замкнутая восьмизвенная ломаная,
вершины которой совпадают со всеми вершинами куба. Какое наименьшее
число звеньев этой ломаной может совпадать с ребрами куба?
Задача 6:
Можно ли, используя каждую из 10 цифр ровно один раз, записать
натуральное число и его квадрат?
Задача 7:
Известно, что корнями квадратного трехчлена f(x) = ax² + bx + c
являются
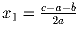
и
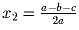
. Докажите,
что один из корней по модулю равен 1.
Задача 8:
Капитан Кук попал на остров, каждый из ста жителей которого либо
лжец, который всегда врет, либо рыцарь, который всегда говорит
правду. Кук узнал, что среди туземцев есть хотя бы один лжец.
Оказалось, что каких 50 жителей ни собери вместе, имеющиеся среди них
лжецы могут сговориться лгать таким образом, что на вопрос «Сколько
среди собранных здесь туземцев рыцарей?" Кук всегда получит один и
тот же набор из 50 ответов. Какое наибольшее число рыцарей могло быть
на острове?


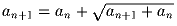 при всех n ≥ 1. Найдите
a1998.
Задача 2:
Внутри выпуклого пятиугольника ABCDE взята точка M. Может ли
оказаться, что каждая из прямых MA, MB, MC, MD, ME отсекает
от пятиугольника ABCDE треугольник?
Задача 3:
Сергей Геннадьевич, взяв менее 100 рублей, пошел гулять. Заходя в
какое-либо кафе и имея при этом m рублей n копеек, он тратил
n рублей m копеек. Какое наибольшее число кафе мог посетить
Сергей Геннадьевич?
Задача 4:
AD и BC – основания равнобедренной трапеции ABCD, O –
точка пересечения ее диагоналей. Докажите, что окружности,
описанные около треугольников ABO и COD пересекаются в центре
окружности, описанной около трапеции ABCD.
Задача 5:
На поверхности куба проведена замкнутая восьмизвенная ломаная,
вершины которой совпадают со всеми вершинами куба. Какое наименьшее
число звеньев этой ломаной может совпадать с ребрами куба?
Задача 6:
Можно ли, используя каждую из 10 цифр ровно один раз, записать
натуральное число и его квадрат?
Задача 7:
Известно, что корнями квадратного трехчлена f(x) = ax² + bx + c
являются
при всех n ≥ 1. Найдите
a1998.
Задача 2:
Внутри выпуклого пятиугольника ABCDE взята точка M. Может ли
оказаться, что каждая из прямых MA, MB, MC, MD, ME отсекает
от пятиугольника ABCDE треугольник?
Задача 3:
Сергей Геннадьевич, взяв менее 100 рублей, пошел гулять. Заходя в
какое-либо кафе и имея при этом m рублей n копеек, он тратил
n рублей m копеек. Какое наибольшее число кафе мог посетить
Сергей Геннадьевич?
Задача 4:
AD и BC – основания равнобедренной трапеции ABCD, O –
точка пересечения ее диагоналей. Докажите, что окружности,
описанные около треугольников ABO и COD пересекаются в центре
окружности, описанной около трапеции ABCD.
Задача 5:
На поверхности куба проведена замкнутая восьмизвенная ломаная,
вершины которой совпадают со всеми вершинами куба. Какое наименьшее
число звеньев этой ломаной может совпадать с ребрами куба?
Задача 6:
Можно ли, используя каждую из 10 цифр ровно один раз, записать
натуральное число и его квадрат?
Задача 7:
Известно, что корнями квадратного трехчлена f(x) = ax² + bx + c
являются 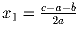 и
и 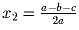 . Докажите,
что один из корней по модулю равен 1.
Задача 8:
Капитан Кук попал на остров, каждый из ста жителей которого либо
лжец, который всегда врет, либо рыцарь, который всегда говорит
правду. Кук узнал, что среди туземцев есть хотя бы один лжец.
Оказалось, что каких 50 жителей ни собери вместе, имеющиеся среди них
лжецы могут сговориться лгать таким образом, что на вопрос «Сколько
среди собранных здесь туземцев рыцарей?" Кук всегда получит один и
тот же набор из 50 ответов. Какое наибольшее число рыцарей могло быть
на острове?
. Докажите,
что один из корней по модулю равен 1.
Задача 8:
Капитан Кук попал на остров, каждый из ста жителей которого либо
лжец, который всегда врет, либо рыцарь, который всегда говорит
правду. Кук узнал, что среди туземцев есть хотя бы один лжец.
Оказалось, что каких 50 жителей ни собери вместе, имеющиеся среди них
лжецы могут сговориться лгать таким образом, что на вопрос «Сколько
среди собранных здесь туземцев рыцарей?" Кук всегда получит один и
тот же набор из 50 ответов. Какое наибольшее число рыцарей могло быть
на острове?