 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Личная олимпиада >> 8 класс | Показать решения |
|
|
| XV Уральский (VIII кировский) турнир юных математиков. Личная олимпиада. 8 класс |
|
|
(Р.Женодаров)
Задача 2: У Васи и Пети по 55 гирь весом 1, 2, …, 55 кг. Они по очереди подкладывают свои гири – каждый на свою чашу двухчашечных весов – причем первым ходит Вася. Петя выигрывает, если разность масс гирь на чашах окажется равной 50 кг. Сможет ли он этого добиться?
(Ю.Лифшиц)
Задача 3: Пусть S(n) – сумма цифр числа n. Найдите все n, для которых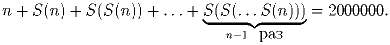
(О.Нечаева)
Задача 4: В треугольнике ABC ∠ A = 3 ∠ C. Точка D на стороне BC обладает тем свойством, что ∠ ADC = 2 ∠ C. Доказать, что AB + AD = BC.
(С.Берлов)
Задача 5: Имеется n дискеток и n этикеток, раскрашенные в несколько цветов. Дубль – это дискета, к которой приклеена этикетка того же цвета. Докажите, что можно добиться того, что все дубли будут одного цвета.(А.Шапиро)
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Личная олимпиада >> 8 класс | Показать решения |