Задача 1:
Задача 2: На плоскости даны окружность ω , точка A, лежащая внутри
ω , и точка B, отличная от A. Рассматриваются всевозможные
треугольники BXY, такие что точки X и Y лежат на ω и
хорда XY проходит через точку A.
Докажите, что центры окружностей, описанных около треугольников BXY,
лежат на одной прямой.
Задача 3:
В пространстве даны n точек общего положения (никакие три не лежат
на одной прямой, никакие четыре не лежат в одной плоскости,
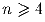
).
Через каждые три из них проведена плоскость. Докажите, что какие бы
n – 3 точки в пространстве ни взять, найдётся плоскость из проведённых,
не содержащая ни одной из этих n – 3 точек.
(В.Дольников, С.Игонин)
Задача 4:
Задача 5:
Существуют ли 10 различных целых чисел таких, что все суммы, составленные
из 9 из них — точные квадраты?
(Р.Садыков, Е.Черепанов)
Задача 6:
В треугольник ABC вписана окружность, касающаяся
сторон AB, AC и BC в точках C
1, B
1 и A
1 соответственно.
Пусть K —
точка на окружности, диаметрально противоположная точке C
1, D — точка
пересечения прямых B
1C
1 и A
1K. Докажите, что CD = CB
1.
(М.Евдокимов)
Задача 7:
Каждый голосующий на выборах вносит в избирательный бюллетень фамилии n
кандидатов. На избирательном участке находится n + 1 урна. После выборов
выяснилось, что в каждой урне лежит по крайней мере один бюллетень и
при всяком выборе (n + 1)-го бюллетеня по одному из каждой урны
найдётся кандидат,
фамилия которого встречается в каждом из выбранных бюллетеней. Докажите, что
по крайней мере в одной урне все бюллетени содержат фамилию одного и того же
кандидата.
(В.Дольников)
Задача 8:
Некоторые натуральные числа отмечены.
Известно, что на каждом отрезке числовой прямой длины 1999 есть отмеченное число.
Докажите, что найдётся пара отмеченных чисел, одно из которых делится на другое.
(С.Берлов)


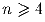 ).
Через каждые три из них проведена плоскость. Докажите, что какие бы
n – 3 точки в пространстве ни взять, найдётся плоскость из проведённых,
не содержащая ни одной из этих n – 3 точек.
).
Через каждые три из них проведена плоскость. Докажите, что какие бы
n – 3 точки в пространстве ни взять, найдётся плоскость из проведённых,
не содержащая ни одной из этих n – 3 точек.