Задача 1:
Найти диагонали вписанного четырехугольника, если
известны все его стороны.
Задача 2:
Треугольник A
1B
1C
1 находится внутри треугольника
A
2B
2C
2, r
1 и r
2 – радиусы их вписанных
окружностей
(соответственно). Доказать, что r
1 ≤ r
2.
Задача 3:
Пусть P(x) – многочлен с целыми коэффициентами,
причем P(1991) = P(1992) = 1993. Доказать, что уравнение
P(x) = 0 не имеет целых корней.
Задача 4:
Сумма неотрицательных чисел a, b и c равна 1.
Доказать, что
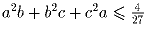
. Исследовать
случай равенства.
Задача 5:
Из 6 различных элементов образованы 30 различных
множеств, причем любые два из них имеют непустое
пересечение. Доказать, что из этих элементов можно
образовать еще одно множество, так чтобы все 31 получившиеся
множества удовлетворяли тем же условиям.


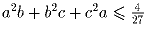 . Исследовать
случай равенства.
. Исследовать
случай равенства.