 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1981, Симферополь >> 10 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1981, Симферополь. 10 класс |
|
|
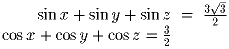
Задача 2: Доказать, что площадь фигуры, ограниченной осями Ox, Oy, прямой
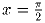 и графиком функции
и графиком функции 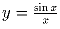 , не меньше 1.
, не меньше 1.Задача 3: На сфере единичного радиуса расположены n ≥ 2 точек. Доказать, что сумма квадратов длин всех отрезков, определяемых этими точками, не превышает n². Может ли она быть равна n² ?
Задача 4: Последовательность неотрицательных чисел an такова, что
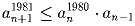
Задача 5: Доказать, что если для всех x из интервала ( – 1;1) выполняется неравенство |a1 sin b1x + a2 sin b2x + … + an sin bnx| ≤ | sin x|, то |a1b1 + a2b2 + … + anbn| ≤ 1.
Задача 6: На доске написан многочлен третьей степени. Ученики по очереди подходят к доске. Каждому из них разрешается заменить написанный на доске многочлен суммой или разностью этого многочлена и его производной. В конце на доске оказался записанным тот жк самый многочлен, с которого начинали. Доказать, что хотя бы один из учеников ошибся, когда писал на доске свой многочлен.
Задача 7: Существует ли многочлен P(x) с целыми коэффициентами такой, что P(19) = P(81) = 1981, а P(1981) равно 19 или 81?
Задача 8: Доказать, что квадратную таблицу 2n × 2n можно заполнить числами – 1, 0, +1 так, чтобы все суммы, которые мы получим, вычисляя сумму всех чисел каждой строки и каждого столбца, были разными.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1981, Симферополь >> 10 класс | Показать решения |