 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1982, Николаев >> 10 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1982, Николаев. 10 класс |
|
|
Задача 2: На плоскости даны правильный n-угольник и вектор
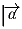 . Найти
сумму ортогональных проекций вектора
. Найти
сумму ортогональных проекций вектора 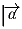 на стороны n-угольника или их
продолжения.
на стороны n-угольника или их
продолжения.Задача 3: В ЭВМ заложена программа, в соответствии с которой любой набор из 10 символов переставляется в определенном порядке, одном и том же для всех наборов. Какое наименьшее число наборов из нулей и единиц нужно составить, чтобы по результатам работы с ними ЭВМ можно было бы однозначно восстановить действие программы? Что это за наборы?
Задача 4: Функция f(x), заданная на отрезке [\,0;1], для любых a,\,b ∈ [\,0;1] удовлетворяет неравенству
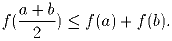
а) Доказать, что уравнение f(x) = 0 имеет бесконечное число решений.
б) Привести пример такой функции, тождественно не равной нулю.
Задача 5: Доказать, что для произвольных значений α , β , γ хотя бы одно из чисел sin α • cos β , sin β • cos γ , sin γ • cos α не больше ½.
Задача 6: Доказать, что если 2a + 3b + 6c = 0, то квадратное уравнение ax² + bx + c = 0 имеет хотя бы один корень на интервале (0;1).
Задача 7: Из точки O проведены лучи OA, OB, OC, образующие между собой острые углы. Прямая a лежит в плоскости OBC и перпендикулярна OA, прямая b лежит в плоскости OAC и перпендикулярна OB, прямая c лежит в плоскости OAB и перпендикулярна OC. Доказать, что прямые a, b, c лежат в одной плоскости.
Задача 8: На плоскости даны n точек, никакие три из которых не лежат на одной прямой. Двое игроков играют в такую игру: каждый по очереди соединяет какую-нибудь пару точек отрезком, причём он не должен пересекаться с проведенным ранее отрезками (но может иметь с ними общие концы). Проигрывает тот, кто не сможет сделать ход. В первой игре выиграл тот, кто начинал игру. Доказать, что он выиграет и в следующей игре.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1982, Николаев >> 10 класс | Показать решения |