Задача 1: От точки O на плоскости отложены три вектора. Известно, что длина суммы любых двух из этих векторов больше, чем длина каждого из векторов-слагаемых. Доказать, что через точку O можно провести прямую так, чтобы все три вектора лежали по одну сторону от этой прямой.

Задача 2: В прямоугольном треугольнике отрезок, соединяющий точку пересечения медиан с основанием биссектрисы, проведенной к катету, перпендикулярен этому катету. Найти углы треугольника.

Задача 3: Многочлен n-й степени f(x) имеет n корней 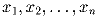, а многочлен (n – 1)-й степени g(x) имеет n – 1 корень , причём x₁ < y₁ < x₂ < y₂ <  …  < y_n – 1 < x_n. Сколько корней может иметь многочлен f(x) + g(x)?

Задача 4: Двадцать пять коротышек делят садовые участки в Цветочном городе. Каждый участок представляет собой квадрат 1 × 1, а все участки вместе — квадрат 5 × 5. Каждый коротышка находится в ссоре не более чем с тремя другими коротышками. Доказать, что участки можно распределить таким образом, чтобы участки поссорившихся коротышек не были бы соседними (соседними называются участки, имеющие общую сторону).

Задача 5: Точки A, B, C и D — вершины выпуклого четырёхугольника. Пять из шести попарных расстояний между парами этих точек равны 1, 1, 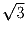, , 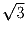3. Найти шестое расстояние.

Задача 6: Отрезок [\,0;1] разбит на части рациональными точками 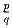, где p и q — натуральные числа и q ≤ 100. Доказать, что среди этих частей найдутся восемь, длина каждой из которых не меньше 0,003.

Задача 7: Улей состоит из решётки шестиугольных сот, все ячейки — правильные шестиугольники одинакового размера и в каждой из ячеек живет одна пчела. Когда пчела A хочет устроить у себя праздник, она начинает жужжать, и все её соседки, которые слышат жужжание, собираются к A в гости. Звук хорошо проходит через 20 стенок сот, но через 21 стенку жужжание уже не слышно. Доказать, что найдутся две пчелы B и C такие, что C находится от A на большем расстоянии, чем B, но C «приходит» на праздник, a B — нет (считать, что каждая пчела находится в центре своей ячейки).

Задача 8: В четвёрке целых чисел a, b, c, d не все числа одинаковы. По этой четвёрке строится новая четвёрка чисел: a₁ = a – b, b₁ = b – c, c₁ = c – d, d₁ = d – a. По четвёрке a₁, b₁, c₁, d₁ тем же способом строится четвёрка a₂, b₂, c₂, d₂ и т.д. Доказать, что хотя бы одно из чисел 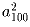, , 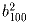, 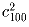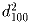больше 10⁹.