 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1988, Луцк >> 10 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1988, Луцк. 10 класс |
|
|
Задача 2: В пространстве дано несколько точек. Никакие 4 из них не лежат в одной плоскости. Если сфера проходит через какие-то 4 из этих точек, то все данные точки лежат в шаре, ограниченном этой сферой. Доказать, что все эти точки лежат на одной сфере.
Задача 3: Пусть P(x,y) — многочлен двух переменных (конечная сумма слагаемых вида axmyn, m ≥ 0, n ≥ 0). Известно, что для любых x и y имеем P(x + 1,y + 1) = P(x,y). Доказать, что существует многочлен одной переменной Q(z) такой, что для любых x и y выполняется равенство P(x,y) = Q(x – y).
Задача 4: Для натуральных n и k, n ≥ k обозначим через
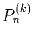 количество разбиений числа n на k натуральных
слагаемых. Разбиения, отличающиеся только порядком слагаемых, считаем
одинаковыми. Например,
количество разбиений числа n на k натуральных
слагаемых. Разбиения, отличающиеся только порядком слагаемых, считаем
одинаковыми. Например,  , так как 4 = 1 + 3 и 4 = 2 + 2.
Доказать, что для n ≥ 2k
, так как 4 = 1 + 3 и 4 = 2 + 2.
Доказать, что для n ≥ 2k 
Задача 5: Доказать, что для произвольных положительных a, b и c выполнено неравенство
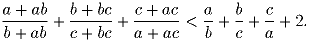
Задача 6: Пусть ABCD — произвольный тетраэдр, K и L — середины противоположных рёбер AD и BC. Через прямую KL проведна некоторая плоскость, пересекающаяся с прямыми AB и CD в точках M1 и M2. Доказать, что точки M1 и M2 равноудалены от прямой KL.
Задача 7: На ограниченном листе бумаги в клетку (с размером клеточек 1 × 1) двое школьников играют в такую игру: сначала первый школьник проводит отрезок A0A1, затем второй школьник — отрезок A1A2, затем первый — A2A3 и т.д.) Каждый из отрезков A0A1, A1A2, A2A3, …должен быть стороной или диагональю клетки, а ломаная A0A1A2A3 … не может иметь самопересечения. Игра прекращается, когда нельзя сделать очередной ход. Доказать, что первый игрок может своими ходами обеспечить, чтобы игра никогда не прекратилась и чтобы расстояние между точками A0 и A1988 оказалось больше 695.
Задача 8:
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1988, Луцк >> 10 класс | Показать решения |