Задача 1:
Вокруг окружности диаметра d описан четырёхугольник, две
противоположные стороны которого равны a и b. Доказать, что ab ≥ d² .
Для каких четырёхугольников имеет место равенство?
Задача 2:
За один шаг последовательность из n чисел
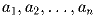
позволяется заменить последовательностью |a
1 – α |,
|a
2 – α |, …, |a
n – α |, где α —
некоторое число (числа α на каждом шаге выбирают произвольно)
В результате таких преобразований необходимо получить
последовательность, все члены которой равны между собой. За какое
наименьшее число шагов это можно сделать?
Задача 3:
Жители страны Полиглотов общаются между собой на 1988 языках.
Каждым языком владеет более половины жителей страны. Доказать, что
можно выбрать 10 жителей так, чтобы каждым из 1988 языков владел хотя
бы один из выбранных жителей.
Задача 4:
В последовательности a
n первый член равен отличному
от 1 натуральному числу a, а каждый член a
n с номером n > 1 удовлетворяет
соотношению
a
n = a
n – ∑
ka
k,
где суммирование в правой части производится по тем индексам k < n, которые
являются делителями n (например, a
10 = a¹º – a
1 – a
2 – a
5). Доказать, что
для каждого натурального n число a
n делится на n.
Задача 5:
Задача 6:
Пусть L и M — середины противоположных сторон AB и
CD четырёхугольника ABCD (не обязательно плоского). Доказать, что
для того, этот четырёхугольник будет трапецией тогда и только тогда,
когда LM = ½(AD + BC).
Задача 7:
Задача 8:
Доказать, что производная функции
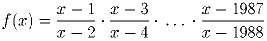
отрицательна во
всех точках, в которых определена функция f(x).


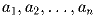 позволяется заменить последовательностью |a1 – α |,
|a2 – α |, …, |an – α |, где α —
некоторое число (числа α на каждом шаге выбирают произвольно)
В результате таких преобразований необходимо получить
последовательность, все члены которой равны между собой. За какое
наименьшее число шагов это можно сделать?
позволяется заменить последовательностью |a1 – α |,
|a2 – α |, …, |an – α |, где α —
некоторое число (числа α на каждом шаге выбирают произвольно)
В результате таких преобразований необходимо получить
последовательность, все члены которой равны между собой. За какое
наименьшее число шагов это можно сделать?