Задача 1:
Сумма всех членов арифметической прогрессии
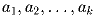
, где
k ≥ 92, равна 1992. Какие значения может принимать сумма a
19 + a
92 в зависимости от k?
Задача 2:
а)
На каждой грани непрозрачного куба написано некоторое натуральное
число. Если несколько граней куба (одну, две или три) можно увидеть
одновременно, то выписываем сумма чисел, написанных на этих гранях. Какое
наибольшее количество различных чисел можно выписать?
б) Какое наименьшее значение при этом может принимать наибольшая из сумм?
Задача 3:
Пусть f(x) — многочлен с целыми коэффициентами. Доказать,
что если ни одно из чисел f(0), f(1), …, f(1991) не делится
на 1992, то многочлен f(x) не имеет целых корней.
Задача 4:
На данной окружности выбрана точку A, а внутри окружности
— точка D. Найти геометрическое место точек пересечения медиан
треугольников ABC, вершины B и C которых лежат на окружности, а
сторона BC проходит через точку D.
Задача 5:
Двое игроков по очереди ставят на клетки шахматной доски 25 × 25 фишки, один — белого, а другой — чёрного цвета. Каждая
новая фишка ставится на свободную клетку, запрещается лишь ставить
фишку на такую клетку, для которой на всех соседних с ней клетках уже
стоят фишки этого же цвета (соседними считаются фишки, имеющие общую
сторону). Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре – начинающий игру или его партнёр?
Задача 6:
Найти все простые числа p < 1000, для которых 2p + 1 будет
степенью натурального числа (то есть выполнено равенство 2p + 1 = m
n, где
m и n — натуральные числа и n > 1).
Задача 7:
Можно ли правильный 1992-угольник разрезать на
параллелограммы?
Задача 8:
Проверить, что окружность x² + 2x + y² = 1992 проходит через
точку (42;12) и доказать, что она содержит бесконечное число точек
B(x;y), обе координаты которых рациональны.


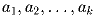 , где
k ≥ 92, равна 1992. Какие значения может принимать сумма a19 + a92 в зависимости от k?
, где
k ≥ 92, равна 1992. Какие значения может принимать сумма a19 + a92 в зависимости от k?